Pythagoras The Father of Music

Excerpts from Mighty Muso - Musings behind Violetta's adventures for adult minds and readers.

Did you see what I did there? ‘Make musical cents?’ I know it’s a bit of a geeky joke, but there is a point. You see, we are about to explore frequencies further, and in order for it to make cents, we need to learn about sense. Or the other way around.

Anyway, there are approximately four cents in a frequency, and an equally tempered semitone is 100 cents. If you are not a musician, you probably have a tonne of questions from that sentence alone; but basically a semitone is the middle distance between two tones, most obvious when you go from a black to a white key on the piano (or white to white in the case where the black is absent).

Now equal temperament is a system of tuning where the octave is divided into twelve semitones. It was invented by Vincenzo Galilei (father of Galileo) in 1581…

Oh, wait. I feel another musical interlude coming on…

‘Galileo, Galileo, Galileo, Galileo, Galileo Figaro...magnifico.’

That’s Queen’s Bohemian Rhapsody by the way, and if you were already singing along, feel free to continue. The head-banging bit/jumping around bit, is especially fun. Queen – Bohemian Rhapsody (Official Video Remastered).

Are you back? Excellent. Well, prior to equal temperament, it was quite difficult for the viols to play with the keyboards, and when all the different instruments of the orchestra began to play together, they had to agree on something. However, we string players experience a slightly grey area when it comes to intonation, attributed to a man named Pythagoras (570 BC - 490 BC).

This ambiguity makes many people shudder, for what that means is a whole lot more anxiety about intonation. Yep, the antagonist in the story of the fretless finger-board—the invisible villain creating a constant battle between the fingers and the ears. Even when the twain meets, it is rocked again by the bigger beast; the ensemble, and, to make matters more complicated, playing in tune varies there too. It depends on whether you are amidst other string players or a pianist. Then there is the symphony orchestra with all the extra timbres. I know. Who would have thunk?

Perhaps I should extrapolate.

What the wise-old Pythagoras is commonly known for—amidst musical circles—is his system of tuning. A system where a scale is constructed using only octaves (that is an interval of eight notes - A to A for instance) and perfect fifths (how violins are tuned - e.g. A to E). In order to assign ratios to each interval, he began playing around with strings, dividing them in half and he started with the earliest stringed instrument called a monchordron, then the lyra and the seven-stringed accordatura—having a string to represent each of the seven planets.

Of course, there were a few differences back in his day. Now we know there are eight planets (nine including Pluto) but from early calculations there were actually only five, as the sun and the moon were included. Anyway, we won’t hold that against Pythagoras. He was still very clever, and his mathematical representations of harmony are still important to know today.

There are many tables that demonstrate this, a lot more succinctly than words, so here is an example.

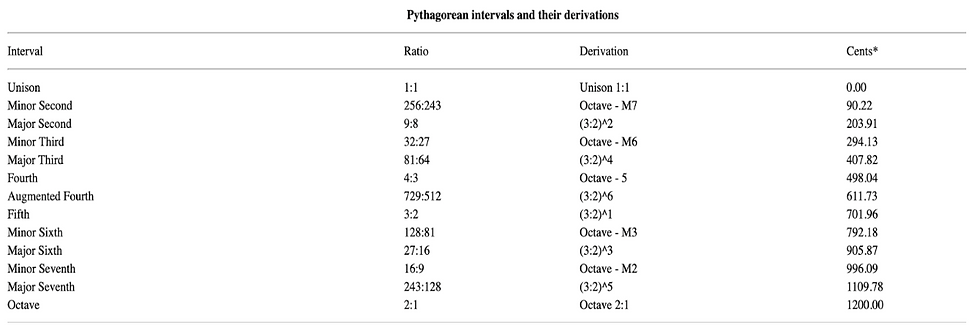
Basically, the unison (1:1) is the strongest interval followed by the octave, so it has the smallest ratio (2:1). The fifth is next (3:2), then the fourth (4:3) as it is an inversion of the fifth. So if you want to know if your E is in tune, you would play it with the A string—not the G string. That would be a major sixth (27:16), and if you did that, you would be flat. Oh, and you know it is in tune because you will not hear beats/pulses between the notes. They are the overtones we talked about a little earlier—heard in the roar of a lion. You don’t really want these to clash. You also wouldn’t want to tune the E against a C. That would be a major third (81:64). Unless you were playing thirds together, in which case, you would tune your E to the A string, and then tune the C to the E. Now if you were tuning against a minor interval, an augmented sixth (59049:32768), or a tritone or a seventh...

Are you still there? Hello?

Honestly, don’t worry. That’s not what we’re here for. We are here to explore the wonders of doing something so difficult, and Pythagoras the father of music, tried to make life a little easier. The upside is that if you do play a stringed instrument, the vibrations of the fundamental frequency are stronger when it is in tune. I also believe it is those waves that make sound almost visible, hovering in the air, suspended somehow from the sky.

Pythagoras thought about the sky too, or the Universus Mundi. Even the word is inspiring, don’t you think?

The word universe is defined by the Oxford dictionary as: ‘All existing matter and space considered as a whole; the cosmos. The universe is believed to be at least 10 billion light years in diameter and contains a vast number of galaxies; it has been expanding since its creation in the Big Bang about 13 billion years ago.’

Does anyone else think of the film Austin Powers at the mention of the word ‘billion’?

As in: ‘We hold the world ransom for; one hundred billion dollars.’

If you have no idea what I’m talking about and want to watch the full clip on YouTube, you can find it here(Austin Powers - 100 billion dollars).

Anyway…

Pythagoras, the universe, and more particularly the cosmos, or Kosmos. Also, an amazing word and that leads me to his theory of ‘The music of the spheres.’ You see, Pythagoras thought that the sun, the moon, the earth and indeed the whole universe emits its own unique hum. I, for one, don’t think it’s that far-fetched. In fact, as previously mentioned, every organism, every object vibrates at a specific frequency, so why then could it not hum?

The first four numbers forming the ratios in the most consonant intervals: Octave (1:2), the fifth (3:2) and the fourth (4:3) were believed to have something to do with it. The significance of the number four will be discussed shortly; but these tetraktys were meant to be ‘the harmony in which the sirens sing.’

So if we want to communicate with the sirens—who sit on the four corners of the universe—perhaps we need to make melodies out of those notes? Like in Close Encounters of the Third Kind?(Close Encounters of the Third Kind — "Tones"), although they had five.

The trouble is, we are not always ‘in harmony’ with the universe; especially when we are surrounded by fridges and motor-bikes. In Plato’s Timaeus, he mentions the concept of a ‘World Soul’ or an Anima Mundi.

‘When two kinds of bodies quarrel with one another, then the tendency to decomposition continues until the smaller either escapes to its kindred element or becomes one with its conqueror. And this tendency in bodies to condense or escape is a source of motion...Where there is motion, there must be a mover, and where there is a mover, there must be something to move.’

We know vibrations occur due to movement. If we consider a violin, the string is being moved—vibrating through friction and the circulation of air. What is the mover? Well, the obvious answer would be the bow, moved by the player. However, if we consider the violinist and player as one organism moving, then what is being moved? And if we are the smaller body, condensing and escaping, could we be moved, might our feet lift from the ground, and is it possible, we might just float upwards if we concentrate, really hard?

Hmm...

Quotes

“When two kinds of body, quarrel with one another…” Plato, trans. Jowett, B. (1998). Timaeus, section 1.

“The harmony in which the siren’s sing…” Iamblichus, On the Pythagorean life, p82, cited in Brunschwig, J. Lloyd, E.R. (2000) Greek Thought: A guide to Classical Knowledge, p.74.